|
Davidas Hilbertas
Davidas Hilbertas (1862.01.23 1943.02.14) vienas įtakingiausių 19 a. pabaigos ir
20 a. pradžios vokiečių matematikas. Jo vardu pavadinta Hilberto erdvė, viena funkcionalinės analizės pagrindinių sąvokų.
Išgarsėjo 23 matematikos problemų sąrašu (detaliau žr. >>>>>).
Gimė Rytų Prūsijos Wehlau mieste (dabar Znamenskas, netoli Kaliningrado). Baigė licėjų
ir įstojo į Kioningsbergo universitetą. 1885 m., vadovaujant F. von Lindemann'ui, apgynė
daktarinę disertaciją Apie tam tikrų binarinių formų, atskiru atveju apskritimo funkcijų,
invariantines savybes. Šiame universitete jis susidraugavo su Hermanu Minkovskiu.
1886-1895 m. jis profesoriavo tame universitete. 1892 m. vedė Kathe Jerosch (1864-1945),
su kuria susilaukė sūnaus Franz Hilbert (1893-1969). 1895-1930 m. jis buvo
Getingeno universiteto profesoriumi, paskaitas skaitė iki 1933 m., o į valdžią atėjus
naciams gyveno Getingene nusišalinęs nuo universitetinių reikalų. Ten ir mirė 1943 m.
Indėlis matematikai
Jo domėjimąsi galima suskirstyti į periodus:
Invariantų teorija (1885-93);
Skaičių teorija (1893-98);
Geometrijos pagrindai (1898-1902);
Dirichle principas ir susiję diferencialinio skaičiavimo problemos (1900-06);
Integralinių lygčių teorija (1900-10);
Skaičių teorijos Varingo problemos sprendimas (1908-09);
Matematinės fizikos pagrindai (1910-22);
Matematikos loginiai pagrindai (1922-39).
Invariantų teorijoje 1888 m. jis įrodė pagrindinę teoremą apie invariantų sistemos baigtinės bazės egzistavimą.
Prieš 20 m. Paul Gordan'as*), naudodamas sudėtingus (
kompleksinių skaičių) skaičiavimus, įrodė teoremą binarinių formų generatoriams.
Bandymai apibendrinti metodą funkcijoms su daugiau nei du kintamieji nepavyko dėl nepaprasto
skaičiavimų sudėtingumo. Hilbertas suprato, kad reikia surasti visiškai kitokį kelią. Jis parodė,
kad egzistuoja baigtinis generatorių skaičius. Paaiškėjo, kad tai ne algoritminė, o egzistavimo
įrodymo teorema. Savo rezultatus Hilbertas pasiuntė Mathematische Annalen, tačiau juos
recenzavęs P. Gordanas nesuprato revoliucinio Hilberto teoremos pobūdžio ir atmetė straipsnį,
pažymėdamas: Tai teologija, o ne matematika!. Tuo tarpu F. Kleinas suprato
straipsnio svarbą ir garantavo, kad jis bus atspausdintas be pakeitimų. Kitame straipsnyje
Hilbertas išvystė savo metodą, ir galiausiai Gordanas pripažino: Net teologija turi nuopelnų.
1899 m. išspausdintuose Geometrijos pagrinduose duodama formali 21 aksiomos
sistema, kaip papildymas Euklido aksiomoms. Nepriklausomai nuo jo ir tuo pačiu metu
19-metis amerikietis Robert Lee Moore**) paskelbė analogišką geometrijos aksiomų sistemą. Tai
žymėjo perėjimą prie šiuolaikinio aksiomatinio metodo. Hilbertas buvo pirmasis griežtai apibrėžęs svarbias koncepcijas:
tašką, tiesę, plokštumą, priklausomybę (taškų ir plokštumos santykį), buvimą tarp, taškų poros ir kampų kongruentiškumą (sutapimą).
Dirichle principo įrodymas leido pradėti naudoti vadinamuosius tiesinius variacinių skaičiavimų metodus.
Hilberto integralinių lygčių su simetriniu branduoliu teorija yra vienu iš šiuolaikinės funkcionalinės analizės pagrindų,
o ypač naudojama tiesinių operatorių spektrinėje teorijoje. Jis įvedė begalinio matavimo euklidinę erdvė -
vėliau pavadintą Hilberto erdve. Vėliau S. Banachas išplėtė šią koncepciją apibrėždamas Banacho erdvę.
1900 m. Paryžiuje vykusiame Antrajame Matematikų kongrese jis pristatė neišspręstų matematikos problemų sąrašą.
Jame buvo pristatyta mažiau nei pusė visų problemų (pradžioje tik 10; 1, 2, 6, 7, 8, 13, 16, 19, 21 ir 22), kurių
sąrašą jis vėliau išplėtė, kol gavome kanonines 23 problemas. Kai kurios buvo išspręstos netrukus, kitos aptariamos visą 20-ą šimtmetį, o kelios liko neišspręstos iki šiol
(išpręsta 16 problemų, o dar dvi nėra korektiškomis matematinėmis problemomis).
Hilberto problemos buvo labai skirtingos temų ir tikslumo požiūriu. Kai kurios iš jų (pvz., 3 ir 8) buvo suformuluotos pakankamai tiksliai, kad būtų galima
aiškiai atsakyti teigiamai arba neigiamai. Bet kai kurie Hilberto teiginiai nebuvo pakankamai tikslūs konkrečiai problemai apibūdinti, tačiau buvo pakankamai įtaigūs.
Be to yra dvi problemos, kurios ne tik neišspręstos, bet iš tikrųjų gali būti neišsprendžiamos pagal šiuolaikinius standartus (4 ir 6).
Nuo 1912 m., praėjus 3 m. po draugo H. Minkovskio mirties,
jis užsiėmė beveik vien fizikos klausimais. Neabejotinai, susidomėjimas fizika buvo H. Minkovskio nuopelnas.
Hilbertas aiškinosi kinetinę dujų teoriją, tada elementariąją spinduliavimo teoriją ir molekulinę
fiziką. Net prasidėjus karui jis tebeorganizavo seminarus ir kursus, kuriuose buvo nagrinėjami
Einšteino darbai. 1915 m. birželio-liepos mėn. Hilbertas pasikvietė Einšteiną į
Getingeną paskaitų ciklui apie bendrąją reliatyvumo bei gravitacijos teorijas.
Pasikeitimas idėjomis leido suformuluoti galutinę bendrosios reliatyvumo teorijos lauko lygčių formą.
1922 m. Hilbertas užsiėmė matematikos formalizavimu ir metamatematiniu jos neprieštaringumo įrodymu. Kartu su P. Bernaisu parašė dviejų tomų Matematikos pagrindus
(1934; 1939). Tačiau neprieštaringumo problema pasirodė sudėtingesnė. 1931 m. Giodelis
įrodė, kad bet kuri neprieštaringa formali sistema, negali įrodyti savo pilnumo remdamasi tik savo aksiomomis.
Tačiau Hilbertas tikėjo ir matematine intuicija. Jam buvo būdingas tikėjimas neribota žmogaus proto galia, įsitikinimas matematikos ir gamtos mokslų vienybe.
Jo darbų rinkinys (1932-35) baigiasi straipsniu Gamtos pažinimas, o jis šūkiu: Privalom žinoti galėsim gyventi.
1934 m. Vokietijos kultūros ministras paklausė Getingeno matematikos
profesoriaus D. Hilberto, ar Matematikos institutas Getingene nenukentėjo nelikus žydų.
- Nukentėjo? atsakė Hilbertas. Jis nenukentėjo. Jo tiesiog daugiau nebeliko.
Viešbučio paradoksas
Šį su begalybe susijusias problemas iliustruojantį paradoksą pateikė D. Hilbertas (1862-1943).
Viešbutyje, kuriame yra baigtinis kambarių skaičius, kai jie visi užimti, viešbutis negali
apgyvendinti naujų svečių. Dabar įsivaizduokime viešbutį, kuris turi begalinį kambarių skaičių.
Tarkim, kad užimti visi jo kambariai. Tačiau vis tiek galima priimti naują svečią: iš kambario 1
perkelkime gyventoją į kambarį 2, iš 2 į 3 ir t.t. Ir tada naujai atvykusį svečią bus galima
apgyvendinti 1 kambaryje. Toks gyventojų perkėlimas nusako super-darbą.
Tokiu pat būdu galima padaryti vietos ir begaliniam naujų svečių kiekiui iš 1
keliame į 2; iš 2 į 4, iš 3 į 6 ir t.t., kad laisvi liktų visi kambariai su nelyginiais numeriais, į
kukiuos galės įsikelti begalinis naujų svečių kiekis. Tačiau čia ir yra paradokso esmė. Koks
bus svečių kiekis bus viešbutyje, kai prie begalybės prijungsime dar begalybę? Tarkim,
atvyksta begalybė naujų svečių ir užima visus nelyginius kambarius, o visi, kurie buvo užėmę
lyginius, išvyksta. Iš begalybės ką tik atėmėme begalybę ir vis tiek dar liko begalybė.
Svečius apgyvendinsime, ir tada, jei į viešbutį atvyktų ir begalinis autobusų skaičius
kiekvienas jų talpinantis begalybę keleivių: pirmiausia atlaisviname visus nelyginius
kambarius (kaip prieš tai). Tada pirmojo autobuso keleivius apgyvendiname kambariuose
3n (n=1,2,3,
), antrojo autobuso keleivius 5n, ir t.t. A autobuso keleivius
apgyvendindami kambariuose pn (n=1,2,3,
), kai p yra A+1-asis pirminis skaičius pirminių skaičių sekoje (3,5,7,11,13,
.)
Matematiškai, begalinės aibės dalis dydžiu prilygsta pačiai aibei, t.y poaibiai yra to paties. Suskaičiuojamoms aibėms tas žymimas
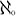 (aleph null). (aleph null).
Įdomu, kad begalinėse aibėse indukcija veikia viena kryptimi. Visi viešbučio svečiai gali
gauti cigarą, tačiau jų nereikia iš niekur atvežti. Kambario 1 gyventojas gaus cigarą iš
kambario 2 gyventojo, šis anksčiau gavo du cigarus iš kambario 3 gyventojo; šis gavo 3 iš kambario 4 ir t.t.
Kai kurie, įrodinėjantys Dievo egzistavimą, (pvz., W. L. Craig) viešbučio paradoksą bandė
panaudoti kaip argumentą, kad tikrovėje begalybė yra negalima. Jie teigia, kad mes intuityviai
žinome, kad tokio viešbučio būti negali. Jie tvirtina, kad laikina seka, be galo tęsiama į praeitį,
gali reikšti tokią realiąją begalybę. Tačiau viešbučio paradoksas apima ne tik begalybę, bet ir
super-darbus. Tuo tarpu priežastinis ryšys be galo tęsiamas į praeitį neapima jokio super-darbo
(Tomo Akviniečio "Summa Theologiae" aptariami amžino judėjimo į praeitį
ir Dievo egzistavimo klausimai).
Panaudojimas literatūroje
Matematiko ir fantasto Rudy Rucker'io romane Baltoji šviesa viešbutis remiasi Hilberto viešbučio paradoksu.
Stephen Baxter fantastiniame romane Trancendentinis yra trumpas begalybės klausimo
aptarimas, panaudojant Hilberto viešbučio paradoksą tik vietoje viešbučio imami tarpžvaigždiniai laivai.
Geoffrey A. Landis garsiajame apsakyme Dirako jūros ratilai Hilberto viešbučio
paradoksas panaudojamas paaiškinimui kodėl sklidina begalinė Dirako jūra vis dar gali talpinti naujas elementariąsias daleles.
Peter Hoeg'o romane Smilos sniego pojūtis herojė samprotauja, kad gerai būtų, jei naujai atvykstantys į viešbutį visada gautų kambarį.
Matematikas ir filosofas Ivar Ekeland'as iliustruotoje knygoje Katinas skaičių šalyje Hilberto
viešbučio paradoksą pristato kaip pasaką vaikams Lewis Carroll stiliumi (iliustratorius John O'Brien).
*) Paulis Gordanas (Paul Albert Gordan, 1837-1912) žydų kilmės vokiečių matematikas,
K. Jakobio mokinys. Kilęs iš Vroclavo (Lenkija). Buvo vadinamas invariantų
karaliumi žinomiausias jo rezultatas tas, kad baigtinio laipsnio binarinių formų invariantų žiedas yra baigtiniu generuotu. Buvo
vienu E. Noether vadovų.
**) Robertas Li Muras (Robert Lee Moore, 1882-1974) amerikiečių matematikas,
pedagogas, žinomas darbais topologijos srityje (tam skyrė vieną monografiją ir
beveik 70 straipsnių) bei eksperimentiniu mokymo metodu, draudžiančiu studentams skaityti vadovėlius ir skatinusiu juos savarankiškai išvesti teorijas.
Buvo rasistiškai priešiškai nusiteikęs prieš juodaodžius studentus. Dar jaunystėje įrodė, kad viena Hilberto aksiomų yra perteklinė.
***) Hilberto erdvė - euklidinės erdvės
apibendrinimas begalinių matavimų realių arba kompleksinių skaičių lauko atvejui.
Svarbiausiu objektu joje yra tiesiniai operatoriai. Pavadinta pagal D. Hilbertą, jos tyrinėjimus pradėjusį 20 a. pradžioje,
o patį pavadinimą įvedė Dž. fon Neimanas darbuose apie ermitinius operatorius.
Kiti HOT.LT straipsniai:
Toji erdvė...
Nulio istorija
Kompiuterių ištakos
Kompiuterių istorija
Didžioji Ferma teorema
Nekritinė stygų teorija
Bendroji reliatyvumo teorija
Klodas Šenonas žmogus, išradęs ateitį
Pirmoji programuotoja: Ada Lovelace
Apie reliatyvumo teorijos prioriteto nustatymą
Vozniakas: pasirinktas gyvenimas šešėlyje
Klasikinės neišsprendžiamos geometrinės konstrukcijos
Bilas Geitsas: kol dar nebuvo garsus
Technika: Nuo Paleolito laikų
Euklidas iš Aleksandrijos
Danas Briklinas: skaičiuoklės autorius
Kibernetikos istorijos etiudai, V. Nalimovas
P-NP: Ant sveiko proto svarstyklių
Algoritmų pirmeivis laimėjo Kyoto premiją
O jei Napoleonas nebūtų panaikinęs dešimtainio laiko?
Styvo Džobso kelias į žvaigždes
Negirdima melodija
ARPANET istorija
Programavimo kalbų evoliucija
Ar mašina kada nors mąstys?
Įsilaužimų istorija
Užmirškite Internetą mokyklose
Eliza ir rūpesčiai dėl tapatybės
Apžvalga: privatumas Internete
| 